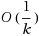Combining Lagrangian decomposition and excessive gap smoothing technique for solving large‐scale separable convex optimization problems

A new algorithm for solving large‐scale convex optimization problems with a separable objective function is proposed. The basic idea is to combine three techniques: Lagrangian dual decomposition, excessive gap and smoothing. The main advantage of this algorithm is that it automatically and simultaneously updates the smoothness parameters which significantly improves its performance. The convergence of the algorithm is proved under weak conditions imposed on the original problem. The rate of convergence is $O(\frac{1}{k})$ , where k is the iteration counter. In the second part of the paper, the proposed algorithm is coupled with a dual scheme to construct a switching variant in a dual decomposition framework. We discuss implementation issues and make a theoretical comparison. Numerical examples confirm the theoretical results.