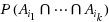Computing bounds for the probability of the union of events by different methods

Let A 1,…,A n be arbitrary events. The underlying problem is to give lower and upper bounds on the probability P(A 1∪…∪A n ) based on 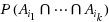$P(A_{i_1}\cap \cdots \cap A_{i_k})$ , 1≤i 1<…<i k ≤n, where k=1,…,d, and d≤n (usually d≪n) is a certain integer, called the order of the problem or the bound. Most bounding techniques fall in one of the following two main categories: those that use (hyper)graph structures and the ones based on binomial moment problems. In this paper we compare bounds from the two categories with each other, in particular the bounds yielded by univariate and multivariate moment problems are compared with Bukszár’s hypermultitree bounds. In the comparison we considered several numerical examples, most of which have important practical applications, e.g., the approximation of the values of multivariate cumulative distribution functions or the calculation of network reliability. We compare the bounds based on how close they are to the real value and the time required to compute them, however, the problems arising in the implementations of the methods as well as the limitations of the usability of the bounds are also illustrated.