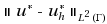| Article ID: | iaor20122780 |
| Volume: | 51 |
| Issue: | 2 |
| Start Page Number: | 883 |
| End Page Number: | 908 |
| Publication Date: | Mar 2012 |
| Journal: | Computational Optimization and Applications |
| Authors: | Wachsmuth Daniel, Beuchler Sven, Pechstein Clemens |
| Keywords: | discrete geometry, error analysis, graphical methods |
We investigate the discretization of optimal boundary control problems for elliptic equations on two‐dimensional polygonal domains by the boundary concentrated finite element method. We prove that the discretization error