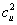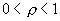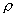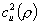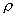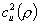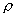The paper proposes an enhancement to the parametric-decomposition method for calculating approximate steady-state performance measures of open queueing networks with non-Poisson arrival processes and nonexponential service-time distributions. Instead of using a variability parameter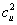 
for each arrival process, it suggests using a variability function 
, 
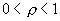for each arrival process; i.e., the variability parameter should be regarded as a function of the traffic intensity 
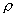of a queue to which the arrival process might go. Variability functions provide a convenient representation of different levels of variability in different time scales for arrival processes that are not nearly renewal processes. Variability functions enable the approximations to account for long-range effects in queueing networks that cannot be addressed by variability parameters, For example, the variability functions provide a way to address the heavy-traffic bottleneck phenomenon, in which exceptional variability (either high or low) in the input has little impact in a series of queues with low-to-moderate traffic intensities, and then has a big impact when it reaches a later queue with a relatively high traffic intensity. The variability functions also enable the approximations to characterize irregular periodic deterministic external arrival processes in a reasonable way; i.e., if there are no batches, then 
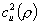should be 0 for 
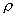near 0 or 1, but 
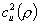can assume arbitrarily large values for appropriate intermediate 
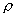. The paper presents a full network algorithm with variability functions, showing that the idea is implementable. It also shows how simulations of single queues can be effectively exploited to determine variability functions for difficult external arrival process.
