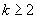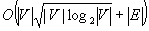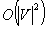| Article ID: | iaor19962212 |
| Country: | Japan |
| Volume: | J78-A |
| Issue: | 12 |
| Start Page Number: | 1627 |
| End Page Number: | 1636 |
| Publication Date: | Dec 1995 |
| Journal: | Transactions of the Institute of Electronics, Information and Communication Engineers |
| Authors: | Wada Koichi, Kawaguchi Kimio, Takaki Akinari |
| Keywords: | computational analysis |
This paper describes efficient algorithms for partitioning a