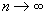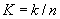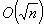| Article ID: | iaor19951492 |
| Country: | Japan |
| Volume: | 36 |
| Issue: | 4 |
| Start Page Number: | 243 |
| End Page Number: | 253 |
| Publication Date: | Dec 1993 |
| Journal: | Journal of the Operations Research Society of Japan |
| Authors: | Moriguti Sigeiti |
| Keywords: | decision theory, combinatorial analysis, simulation |
Selection from among