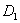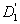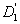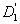A new triangulation for simplicial algorithms

Triangulations are used in simplicial algorithms to find the fixed points of continuous functions or upper semicontinuous mappings; applications arise from economics and optimization. The performance of simplicial algorithms is very sensitive to the triangulation used. Using a facetal description, Dang's triangulation is modified to obtain a more efficient triangulation of the unit hypercube in Rⁿ, and then, by means of translations and reflections, a new triangulation, , of Rⁿ is derived. It is shown that uses fewer simplices (asymptotically 30 percent fewer) than D 1 while achieving comparable scores for other performance measures such as the diameter and the surface density. The results of Haiman's recursive method for getting asymptotically better triangulations from D1 , and other triangulations are also compared.