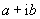The connections between the Golden Ratio namely 
, a simple continued fraction, and Fibonacci and Lucas numbers, are familiar. The Fibonacci and Lucas numbers have many fascinating properties. The paper now points out that the square root of the Golden Ratio is the real part of a simple periodic continued fraction but using (complex) Gaussian integers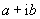 
instead of the natural integers. This fact provokes a definition and a study of complex Fibonacci and Lucas numbers, and the study again turns out to have a rich theoretic structure. A fuller account will appear in The Fibonacci Quarterly.
