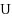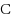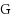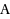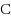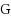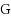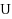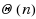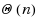Combinatorial RNA Design: Designability and Structure-Approximating Algorithm in Watson‐Crick and Nussinov‐Jacobson Energy Models

We consider the Combinatorial RNA Design problem, a minimal instance of RNA design where one must produce an RNA sequence that adopts a given secondary structure as its minimal free‐energy structure. 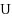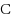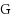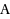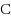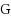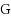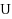We consider two free‐energy models where the contributions of base pairs are additive and independent: the purely combinatorial Watson–Crick model, which only allows equally‐contributing $‐{A}$ – $‐{U}$ and $‐{C}$ – $‐{G}$ base pairs, and the real‐valued Nussinov–Jacobson model, which associates arbitrary energies to $‐{A}$ – $‐{U}$ , $‐{C}$ – $‐{G}$ and $‐{G}$ – $‐{U}$ base pairs. We first provide a complete characterization of designable structures using restricted alphabets and, in the four‐letter alphabet, provide a complete characterization for designable structures without unpaired bases. When unpaired bases are allowed, we characterize extensive classes of (non‐)designable structures, and prove the closure of the set of designable structures under the stutter operation. Membership of a given structure to any of the classes can be tested in 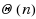$\mathit{\Theta }(n)$ time, including the generation of a solution sequence for positive instances. Finally, we consider a structure‐approximating relaxation of the design, and provide a 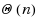$\mathit{\Theta }(n)$ algorithm which, given a structure S that avoids two trivially non‐designable motifs, transforms S into a designable structure constructively by adding at most one base‐pair to each of its stems.