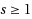We analyze a discrete‐time queueing model where two types of customers, each having their own dedicated server, are accommodated in one single FCFS queue. Service times are deterministically equal to
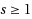time slots each. New customers enter the system according to a general independent arrival process, but the types of consecutive customers may be nonindependent. As a result, arriving customers may (or may not) have the tendency to cluster according to their types, which may lead to more (or less) blocking of one type by the opposite type. The paper reveals the impact of this blocking phenomenon on the achievable throughput, the (average) system content, the (average) customer delay and the (average) unfinished work. The paper extends the results of earlier work where either the service times were assumed to be constant and equal to 1 slot each, or the customers all belonged to the same class. Our results show that, in case of Poisson arrivals, for given traffic intensity, the system‐content distribution is insensitive to the length (s) of the service times, but the (mean) delay and the (mean) unfinished work in the system are not. In case of bursty arrivals, we find that all the performance measures are affected by the length (s) of the service times, for given traffic intensity.
