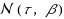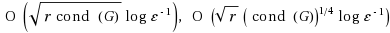| Article ID: | iaor20173358 |
| Volume: | 68 |
| Issue: | 1 |
| Start Page Number: | 29 |
| End Page Number: | 55 |
| Publication Date: | Sep 2017 |
| Journal: | Computational Optimization and Applications |
| Authors: | Mansouri H, Zangiabadi M, Sayadi Shahraki M |
| Keywords: | heuristics |
In this paper, we present two primal–dual interior‐point algorithms for symmetric cone optimization problems. The algorithms produce a sequence of iterates in the wide neighborhood