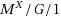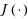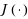| Article ID: | iaor20172890 |
| Volume: | 86 |
| Issue: | 3 |
| Start Page Number: | 217 |
| End Page Number: | 240 |
| Publication Date: | Aug 2017 |
| Journal: | Queueing Systems |
| Authors: | Nez-Queija Rudesindo, Boon Marko A A, Boxma Onno J, Abhishek |
| Keywords: | queues: applications, markov processes, service |
We investigate the transient and stationary queue length distributions of a class of service systems with correlated service times. The classical