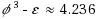Non-preemptive buffer management for latency sensitive packets

The delivery of latency sensitive packets is a crucial issue in real‐time applications of communication networks. Such packets often have a firm deadline and a packet becomes useless if it arrives after its deadline. The deadline, however, applies only to the packet’s journey through the entire network; individual routers along the packet’s route face a more flexible deadline. We study policies for admitting latency sensitive packets at a router. Each packet is tagged with a value. A packet waiting at a router loses value over time as its probability of arriving at its destination on time decreases. The router is modeled as a non‐preemptive queue, and its objective is to maximize the total value of the forwarded packets. When a router receives a packet, it must either accept it (and delay future packets), or reject it immediately. The best policy depends on the set of values that a packet can take. We consider three natural sets: an unrestricted model, a real‐valued model, where any value over 1 is allowed, and an integral‐valued model. For the unrestricted model, we prove that there is no constant competitive ratio algorithm. For the real‐valued model, we give a randomized 4‐competitive algorithm and a matching lower bound (up to low order terms). We also provide a deterministic lower bound of ${\mathit{\varphi }}^3‐\mathit{ϵ}\approx 4.236$ , almost matching the previously known 4.24‐competitive algorithm. For the integral‐valued model, we describe a deterministic 4‐competitive algorithm, and prove that this is tight even for randomized algorithms (up to low order terms).