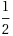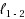Further properties of the forward‐backward envelope with applications to difference-of-convex programming

In this paper, we further study the forward–backward envelope first introduced in Patrinos and Bemporad (Proceedings of the IEEE Conference on Decision and Control, pp 2358–2363, 2013) and Stella et al. (Comput Optim Appl, doi: ‐10.1007/s10589-017-9912-y, 2017) for problems whose objective is the sum of a proper closed convex function and a twice continuously differentiable possibly nonconvex function with Lipschitz continuous gradient. We derive sufficient conditions on the original problem for the corresponding forward–backward envelope to be a level‐bounded and Kurdyka–Łojasiewicz function with an exponent of 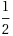$\frac{1}{2}$ ; these results are important for the efficient minimization of the forward–backward envelope by classical optimization algorithms. In addition, we demonstrate how to minimize some difference‐of‐convex regularized least squares problems by minimizing a suitably constructed forward–backward envelope. Our preliminary numerical results on randomly generated instances of large‐scale 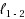${\ell }_{1‐2}$ regularized least squares problems (Yin et al. in SIAM J Sci Comput 37:A536–A563, 2015) illustrate that an implementation of this approach with a limited‐memory BFGS scheme usually outperforms standard first‐order methods such as the nonmonotone proximal gradient method in Wright et al. (IEEE Trans Signal Process 57:2479–2493, 2009).