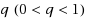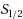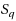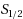S1/2 regularization methods and fixed point algorithms for affine rank minimization problems

The affine rank minimization problem is to minimize the rank of a matrix under linear constraints. It has many applications in various areas such as statistics, control, system identification and machine learning. Unlike the literatures which use the nuclear norm or the general Schatten $q(0<q<1)$ quasi‐norm to approximate the rank of a matrix, in this paper we use the Schatten 1 / 2 quasi‐norm approximation which is a better approximation than the nuclear norm but leads to a nonconvex, nonsmooth and non‐Lipschitz optimization problem. It is important that we give a global necessary optimality condition for the $S_{1/2}$ regularization problem by virtue of the special objective function. This is very different from the local optimality conditions usually used for the general $S_q$ regularization problems. Explicitly, the global necessary optimality condition for the $S_{1/2}$ regularization problem is a fixed point inclusion associated with the singular value half thresholding operator. Naturally, we propose a fixed point iterative scheme for the problem. We also provide the convergence analysis of this iteration. By discussing the location and setting of the optimal regularization parameter as well as using an approximate singular value decomposition procedure, we get a very efficient algorithm, half norm fixed point algorithm with an approximate SVD (HFPA algorithm), for the $S_{1/2}$ regularization problem. Numerical experiments on randomly generated and real matrix completion problems are presented to demonstrate the effectiveness of the proposed algorithm.