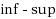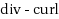A saddle point least squares approach to mixed methods

We investigate new PDE discretization approaches for solving variational formulations with different types of trial and test spaces. The general mixed formulation we consider assumes a stability LBB condition and a data compatibility condition at the continuous level. We expand on the Bramble–Pasciak’s least square formulation for solving such problems by providing new ways to choose approximation spaces and new iterative processes to solve the discrete formulations. Our proposed method has the advantage that a discrete $inf‐sup$ condition is automatically satisfied by natural choices of test spaces (first) and corresponding trial spaces (second). In addition, for the proposed iterative solver, a nodal basis for the trial space is not required. Applications of the new approach include discretization of first order systems of PDEs, such as $div‐curl$ systems and time‐harmonic Maxwell equations.