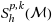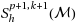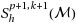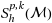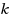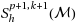| Article ID: | iaor201527788 |
| Volume: | 70 |
| Issue: | 7 |
| Start Page Number: | 1555 |
| End Page Number: | 1582 |
| Publication Date: | Oct 2015 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Kumar Mukesh, Kvamsdal Trond, Johannessen Kjetil Andr |
| Keywords: | error analysis, geometry |
In this article we propose two simple a posteriori error estimators for solving second order elliptic problems using adaptive isogeometric analysis. The idea is based on a