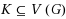Let G denote a graph, and
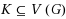represent a set of target vertices. Assume that the non‐target vertices of G fail independently with given probabilities. The K‐terminal reliability of G is defined as the probability that all target vertices in K are connected. Computing K‐terminal reliability is #P‐complete for chordal graphs, yet solvable in polynomial time for its subclass of interval graphs. While improving both of these results, this work demonstrates that although the problem remains #P‐complete when restricted to directed path graphs, a further restriction to rooted directed path graphs yields a polynomial time solution.
