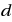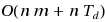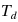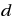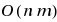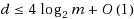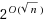| Article ID: | iaor2014862 |
| Volume: | 8 |
| Issue: | 5 |
| Start Page Number: | 1611 |
| End Page Number: | 1617 |
| Publication Date: | Jun 2014 |
| Journal: | Optimization Letters |
| Authors: | Butenko Sergiy, Pardalos Panos, Buchanan Austin, Walteros Jose |
| Keywords: | maximum clique |
We describe an algorithm for the maximum clique problem that is parameterized by the graph’s degeneracy