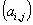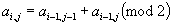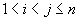| Article ID: | iaor19931490 |
| Country: | Netherlands |
| Volume: | 41 |
| Issue: | 2 |
| Start Page Number: | 165 |
| End Page Number: | 171 |
| Publication Date: | Jan 1993 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Brand Neal, Curran Stephen, Das Sajal, Jacob Tom |
| Keywords: | probability |
A Steinhaus graph is a graph with