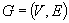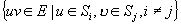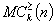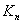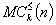| Article ID: | iaor19931480 |
| Country: | United States |
| Volume: | 17 |
| Issue: | 4 |
| Start Page Number: | 981 |
| End Page Number: | 1000 |
| Publication Date: | Nov 1992 |
| Journal: | Mathematics of Operations Research |
| Authors: | Deza M., Grotschel M., Laurent M. |
| Keywords: | combinatorial analysis |
Let