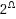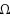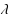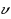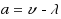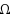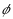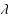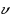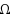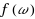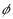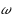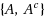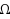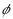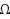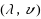Peter Fishburn's analysis of ambiguity

In ordinary discourse the term ambiguity typically refers to vagueness or imprecision in a natural language. Among decision theorists, however, this term usually refers to imprecision in an individual’s probabilistic judgments, in the sense that the available evidence is consistent with more than one probability distribution over possible states of the world. Avoiding a prior commitment to either of these interpretations, Fishburn has explored ambiguity as a primitive concept, in terms of what he calls an ambiguity measure a on the power set 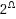$2^{\mathrm{\Omega }}$ of a finite set 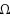$\mathrm{\Omega }$ , characterized by five axioms. 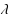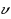We prove, in purely set‐theoretic terms, that if $\mathit{\lambda }$ is a so‐called necessity measure on $2^{\mathrm{\Omega }}$ and $\mathit{\upsilon }$ is its associated possibility measure, then 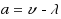$a=\mathit{\upsilon }‐\mathit{\lambda }$ is an ambiguity measure. 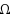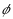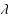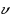When $\mathrm{\Omega }$ is construed as a set of possible exemplars of a vague predicate $\mathit{\varphi }$ , then $\mathit{\lambda }$ and $\mathit{\upsilon }$ may be regarded as arising from a fuzzy membership function f on 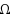$\mathrm{\Omega }$ , where 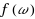$f(\mathit{\omega })$ designates the degree to which 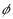$\mathit{\varphi }$ is applicable to 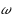$\mathit{\omega }$ . In this case a(A) represents the degree to which the partition 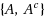$\{A,A^c\}$ differentiates members of 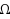$\mathrm{\Omega }$ with respect to the predicate 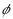$\mathit{\varphi }$ . When 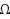$\mathrm{\Omega }$ is construed as a set of possible states of the world, a necessity measure may be regarded as a very special type of lower probability known as a consonant belief function, and a possibility measure as its associated upper probability, whence a(A) represents the degree of imprecision in the pair 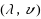$(\mathit{\lambda },\mathit{\upsilon })$ with respect to the event A. Fishburn’s axioms are thus consistent with an interpretation of ambiguity as linguistic vagueness, as well as (a very special sort of) probabilistic imprecision.