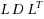On the update of constraint preconditioners for regularized KKT systems

We address the problem of preconditioning sequences of regularized KKT systems, such as those arising in interior point methods for convex quadratic programming. In this case, constraint preconditioners (CPs) are very effective and widely used; however, when solving large‐scale problems, the computational cost for their factorization may be high, and techniques for approximating them appear as a convenient alternative. Here, given a block $LD{L}^T$ factorization of the CP associated with a KKT matrix of the sequence, called seed matrix, we present a technique for updating the factorization and building inexact CPs for subsequent matrices of the sequence. We have recently proposed an updating procedure that performs a low‐rank correction of the Schur complement of the (1,1) block of the CP for the seed matrix. Now we focus on KKT sequences with nonzero (2,2) blocks and make a step further, by enriching the low‐rank correction of the Schur complement by an additional cheap update. The latter update takes into account information not included in the former one and expressed as a diagonal modification of the low‐rank correction. Theoretical results and numerical experiments show that the new strategy can be more effective than the procedure based on the low‐rank modification alone.