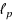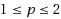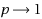Nonlinear residual minimization by iteratively reweighted least squares

In this paper we address the numerical solution of minimal norm residuals of nonlinear equations in finite dimensions. We take particularly inspiration from the problem of finding a sparse vector solution of phase retrieval problems by using greedy algorithms based on iterative residual minimizations in the 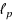${𝓁}_p$ ‐norm, for 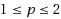$1\le p\le 2$ . Due to the mild smoothness of the problem, especially for 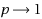$p\to 1$ , we develop and analyze a generalized version of iteratively reweighted least squares (IRLS). This simple and efficient algorithm performs the solution of optimization problems involving non‐quadratic possibly non‐convex and non‐smooth cost functions, which can be transformed into a sequence of common least squares problems. The latter can be tackled eventually by more efficient numerical optimization methods. While its analysis has been by now developed in many different contexts (e.g., for sparse vector, low‐rank matrix optimization, and for the solution of PDE involving p‐Laplacians) when the model equation is linear, no results are up to now provided in case of nonlinear ones. We address here precisely the convergence and the rate of error decay of IRLS for such nonlinear problems. The analysis of the convergence of the algorithm is based on its reformulation as an alternating minimization of an energy functional. In fact its main variables are the competitors to solutions of the intermediate reweighted least squares problems and their weights. Under a specific condition of coercivity often verified in practice and assumptions of local convexity, we are able to show convergence of IRLS to minimizers of the nonlinear residual problem. For the case where we are lacking the local convexity, we propose an appropriate convexification by quadratic perturbations. Eventually we are able to show convergence of this modified procedure to at least a very good approximation of stationary points of the original problem. In order to illustrate the theoretical results we conclude the paper with several numerical experiments. We first compare IRLS with standard Matlab optimization functions for a simple and easily presentable example. Furthermore we numerically validate our theoretical results in the more complicated framework of phase retrieval problems, which are our main motivation. Finally we examine the recovery capability of the algorithm in the context of data corrupted by impulsive noise where the sparsification of the residual is desired.