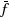This paper presents a trust region algorithm to minimize a function f when one has access only to noise‐corrupted function values
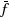. The model‐based algorithm dynamically adjusts its step length, taking larger steps when the model and function agree and smaller steps when the model is less accurate. The method does not require the user to specify a fixed pattern of points used to build local models and does not repeatedly sample points. If f is sufficiently smooth and the noise is independent and identically distributed with mean zero and finite variance, we prove that our algorithm produces iterates such that the corresponding function gradients converge in probability to zero. We present a prototype of our algorithm that, while simplistic in its management of previously evaluated points, solves benchmark problems in fewer function evaluations than do existing stochastic approximation methods.
