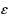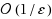A fast dual proximal-gradient method for separable convex optimization with linear coupled constraints

In this paper we consider a class of separable convex optimization problems with linear coupled constraints arising in many applications. Based on Nesterov’s smoothing technique and a fast gradient scheme, we present a fast dual proximal‐gradient method to solve this class of problems. Under some conditions, we then give the convergence analysis of the proposed method and show that the computational complexity bound of the method for achieving an $\mathit{ϵ}$ ‐optimal feasible solution is $\mathcal{O}(1/\mathit{ϵ})$ . To further accelerate the proposed algorithm, we utilize a restart technique by successively decreasing the smoothing parameter. The advantage of our algorithms allows us to obtain the dual and primal approximate solutions simultaneously, which is fast and can be implemented in a parallel fashion. Several numerical experiments are presented to illustrate the effectiveness of the proposed algorithms. The numerical results validate the efficiency of our methods.