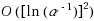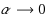The split Bregman algorithm applied to PDE-constrained optimization problems with total variation regularization

We derive an efficient solution method for ill‐posed PDE‐constrained optimization problems with total variation regularization. This regularization technique allows discontinuous solutions, which is desirable in many applications. Our approach is to adapt the split Bregman technique to handle such PDE‐constrained optimization problems. This leads to an iterative scheme where we must solve a linear saddle point problem in each iteration. We prove that the spectra of the corresponding saddle point operators are almost contained in three bounded intervals, not containing zero, with a very limited number of isolated eigenvalues. Krylov subspace methods handle such operators very well and thus provide an efficient algorithm. In fact, we can guarantee that the number of iterations needed cannot grow faster than $O({[ln({\mathit{\alpha }}^{‐1})]}^2)$ as $\mathit{\alpha }\to 0$ , where $\mathit{\alpha }$ is a small regularization parameter. Moreover, in our numerical experiments we demonstrate that one can expect iteration numbers of order $O(ln({\mathit{\alpha }}^{‐1}))$ .