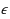Bounding duality gap for separable problems with linear constraints

We consider the problem of minimizing a sum of non‐convex functions over a compact domain, subject to linear inequality and equality constraints. Approximate solutions can be found by solving a convexified version of the problem, in which each function in the objective is replaced by its convex envelope. We propose a randomized algorithm to solve the convexified problem which finds an $\mathit{ϵ}$ ‐suboptimal solution to the original problem. With probability one, $\mathit{ϵ}$ is bounded by a term proportional to the maximal number of active constraints in the problem. The bound does not depend on the number of variables in the problem or the number of terms in the objective. In contrast to previous related work, our proof is constructive, self‐contained, and gives a bound that is tight.