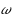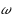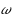| Article ID: | iaor20162325 |
| Volume: | 64 |
| Issue: | 2 |
| Start Page Number: | 535 |
| End Page Number: | 555 |
| Publication Date: | Jun 2016 |
| Journal: | Computational Optimization and Applications |
| Authors: | Kuno Takahito, Ishihama Tomohiro |
| Keywords: | heuristics |
In this paper, we refine the proof of convergence by Kuno–Buckland (J Global Optim 52:371–390, 2012) for the simplicial algorithm with