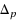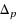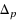Optimal averaged Hausdorff archives for bi-objective problems: theoretical and numerical results

One main task in evolutionary multiobjective optimization (EMO) is to obtain a suitable finite size approximation of the Pareto front which is the image of the solution set, termed the Pareto set, of a given multiobjective optimization problem. In the technical literature, the characteristic of the desired approximation is commonly expressed by closeness to the Pareto front and a sufficient spread of the solutions obtained. In this paper, we first make an effort to show by theoretical and empirical findings that the recently proposed Averaged Hausdorff (or ${\mathrm{\Delta }}_p$ −) indicator indeed aims at fulfilling both performance criteria for bi‐objective optimization problems. In the second part of this paper, standard EMO algorithms combined with a specialized archiver and a postprocessing step based on the ${\mathrm{\Delta }}_p$ indicator are introduced which sufficiently approximate the ${\mathrm{\Delta }}_p$ ‐optimal archives and generate solutions evenly spread along the Pareto front.