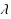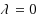| Article ID: | iaor201526335 |
| Volume: | 81 |
| Issue: | 3 |
| Start Page Number: | 269 |
| End Page Number: | 298 |
| Publication Date: | Jun 2015 |
| Journal: | Mathematical Methods of Operations Research |
| Authors: | Cavazos-Cadena Rolando, Chvez-Rodrguez Selene, Cruz-Surez Hugo |
| Keywords: | programming: markov decision, risk, optimization |
This note concerns discrete‐time controlled Markov chains driven by a decision maker with constant risk‐sensitivity