In this paper we are concerned with the following four types of integer problems. Integer Selection Problem (ISP): Let 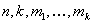 be positive integers and let
be positive integers and let 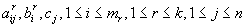 and
and  be given integers. Find an integer
be given integers. Find an integer  with
with 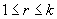 and non-negative integers
and non-negative integers 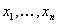 satisfying
satisfying 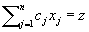 and
and 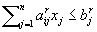 for
for 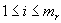 . 3-valued Problem: Given integers
. 3-valued Problem: Given integers 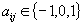 and
and 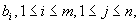 find
find 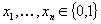 satisfying
satisfying 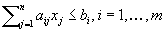 . Indeterminate Coefficient Problem (IDCP): Let m, n, p and q be positive integers,
. Indeterminate Coefficient Problem (IDCP): Let m, n, p and q be positive integers, 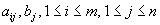 integers, and let
integers, and let  and
and 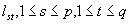 be given integers. Find non-negative integers
be given integers. Find non-negative integers 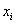 and
and 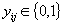 satisfying
satisfying 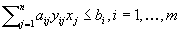 and
and 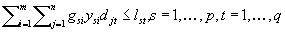 . IDCP with boundedness conditions: Given integers
. IDCP with boundedness conditions: Given integers 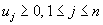 , solve the IDCP under the boundedness conditions
, solve the IDCP under the boundedness conditions 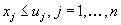 . The main objective in this paper is to show that the two problems ISP and IDCP are equivalent, and that any IDCP with boundedness conditions is reduced to a 3-valued problem, as stated below: Any solution of a given ISP (resp. IDCP and IDCP with boundedness conditions) is derived from solutions of the associated IDCP (resp. ISP and 3-valued problem) and vice versa. In order to state the second result on the 3-valued problem for given integers
. The main objective in this paper is to show that the two problems ISP and IDCP are equivalent, and that any IDCP with boundedness conditions is reduced to a 3-valued problem, as stated below: Any solution of a given ISP (resp. IDCP and IDCP with boundedness conditions) is derived from solutions of the associated IDCP (resp. ISP and 3-valued problem) and vice versa. In order to state the second result on the 3-valued problem for given integers 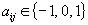 and
and 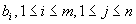 , we introduce two notions: We say that a subset
, we introduce two notions: We say that a subset 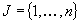 of
of 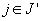 is weakly (resp. strongly) removable, if for each
is weakly (resp. strongly) removable, if for each 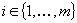 there exists
there exists  satisfying
satisfying  (resp.
(resp. 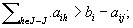 ) and
) and  and we say that
and we say that 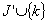 is maximal if
is maximal if 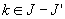 for any
for any 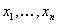 is not weakly (resp. strongly) removable. Using the above terminologies, we may state the following result which provides useful necessary conditions for the existence of solutions of 3-valued problems: Let
is not weakly (resp. strongly) removable. Using the above terminologies, we may state the following result which provides useful necessary conditions for the existence of solutions of 3-valued problems: Let 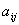 be a solution of the 3-valued problem formulated for
be a solution of the 3-valued problem formulated for  and
and  . (i) If there are no solutions
. (i) If there are no solutions 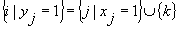 such that
such that 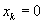 for k with
for k with 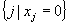 , then the subset
, then the subset 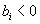 is maximal as a weakly removable set and also maximal as a strongly removable set. (ii) If
is maximal as a weakly removable set and also maximal as a strongly removable set. (ii) If 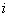 for any
for any 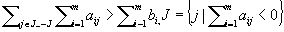 and the inequality
and the inequality  holds for a subset
holds for a subset 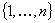 of
of  , than
, than 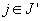 for some
for some .gif) .
.

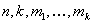
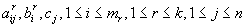
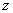
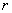
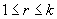
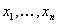
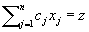
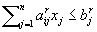
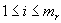
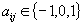
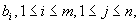
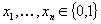
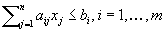
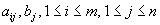

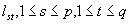
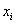
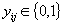
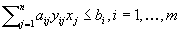
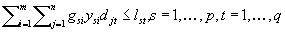
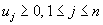
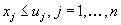
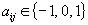
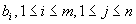
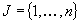
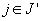
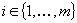


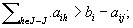

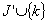
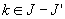
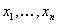
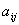


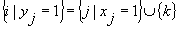
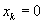
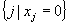
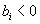
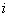
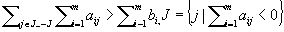

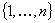

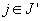
.gif)