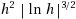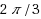Superconvergence for Neumann boundary control problems governed by semilinear elliptic equations

This paper is concerned with the discretization error analysis of semilinear Neumann boundary control problems in polygonal domains with pointwise inequality constraints on the control. The approximations of the control are piecewise constant functions. The state and adjoint state are discretized by piecewise linear finite elements. In a postprocessing step approximations of locally optimal controls of the continuous optimal control problem are constructed by the projection of the respective discrete adjoint state. Although the quality of the approximations is in general affected by corner singularities a convergence order of $h^2{|lnh|}^{3/2}$ is proven for domains with interior angles smaller than $2\mathit{\pi }/3$ using quasi‐uniform meshes. For larger interior angles mesh grading techniques are used to get the same order of convergence.