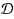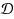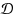Given a set
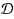of patterns of total length n, the dictionary matching problem is to index
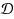such that for any query text T, we can locate the occurrences of any pattern within T efficiently. This problem can be solved in optimal O(|T|+occ) time by the classical AC automaton (Aho and Corasick in Commun. ACM 18(6):333–340, 1975), where occ denotes the number of occurrences. The space requirement is O(n) words which is still far from optimal. In this paper, we show that in many cases, sparsification technique can be applied to improve the space requirements of the indexes for the dictionary matching and its related problems. First, we give a compressed index for dictionary matching, and show that such an index can be generalized to handle dynamic updates of
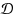. Also, we give a compressed index for approximate dictionary matching with one error. In each case, the query time is only slowed down by a polylogarithmic factor when compared with that achieved by the best O(n)‐word counterparts.
