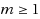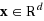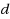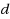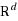A general solution for robust linear programs with distortion risk constraints

Linear optimization problems are investigated that have random parameters in their 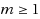$m\ge 1$ constraints. In constructing a robust solution 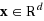$\mathbf{x}\in {‐{R}}^d$ , we control the risk arising from violations of the constraints. This risk is measured by set‐valued risk measures, which extend the usual univariate coherent distortion (=spectral) risk measures to the multivariate case. To obtain a robust solution in 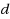$d$ variables, the linear goal function is optimized under the restrictions holding uniformly for all parameters in a 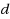$d$ ‐variate uncertainty set. This set is built from uncertainty sets of the single constraints, each of which is a weighted‐mean trimmed region in 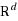${‐{R}}^d$ and can be efficiently calculated. Furthermore, a possible substitution of violations between different constraints is investigated by means of the admissable set of the multivariate risk measure. In the case of no substitution, we give an exact geometric algorithm, which possesses a worst‐case polynomial complexity. We extend the algorithm to the general substitutability case, that is, to robust polyhedral optimization. The consistency of the approach is shown for generally distributed parameters. Finally, an application of the model to supervised machine learning is discussed.