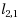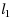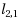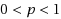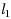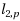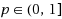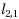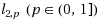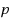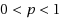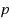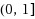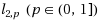A unified algorithm for mixed l2,p-minimizations and its application in feature selection

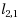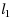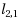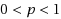Recently, matrix norm $l_{2,1}$ has been widely applied to feature selection in many areas such as computer vision, pattern recognition, biological study and etc. As an extension of $l_1$ norm, $l_{2,1}$ matrix norm is often used to find jointly sparse solution. Actually, computational studies have showed that the solution of $l_p$ ‐minimization ( $0<p<1$ ) is sparser than that of 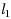$l_1$ ‐minimization. The generalized 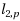$l_{2,p}$ ‐minimization ( 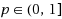$p\in (0,1]$ ) is naturally expected to have better sparsity than 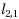$l_{2,1}$ ‐minimization. This paper presents a type of models based on 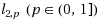$l_{2,p}(p\in (0,1])$ matrix norm which is non‐convex and non‐Lipschitz continuous optimization problem when 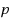$p$ is fractional ( 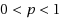$0<p<1$ ). 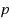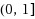For all $p$ in $(0,1]$ , a unified algorithm is proposed to solve the $l_{2,p}$ ‐minimization and the convergence is also uniformly demonstrated. In the practical implementation of algorithm, a gradient projection technique is utilized to reduce the computational cost. 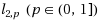Typically different $l_{2,p}(p\in (0,1])$ are applied to select features in computational biology.