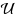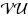The space decomposition theory for a class of eigenvalue optimizations

In this paper we study optimization problems involving eigenvalues of symmetric matrices. One of the difficulties with numerical analysis of such problems is that the eigenvalues, considered as functions of a symmetric matrix, are not differentiable at those points where they coalesce. Here we apply the $𝒰$ ‐Lagrangian theory to a class of D.C. functions (the difference of two convex functions): the arbitrary eigenvalue function λ i , with affine matrix‐valued mappings, where λ i is a D.C. function. We give the first‐and second‐order derivatives of $𝒰$ ‐Lagrangian in the space of decision variables R ^m when transversality condition holds. Moreover, an algorithm framework with quadratic convergence is presented. Finally, we present an application: low rank matrix optimization; meanwhile, list its $\mathrm{𝒱𝒰}$ decomposition results.