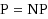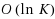Approximating the min‐max (regret) selecting items problem

In this paper the problem of selecting p items out of n available to minimize the total cost is discussed. This problem is a special case of many important combinatorial optimization problems such as 0–1 knapsack, minimum assignment, single machine scheduling, minimum matroid base or resource allocation. It is assumed that the item costs are uncertain and they are specified as a scenario set containing K distinct cost scenarios. In order to choose a solution the min–max and min–max regret criteria are applied. It is shown that both min–max and min–max regret problems are not approximable within any constant factor unless 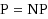$\mathrm{P}=\mathrm{NP}$ , which strengthens the results known up to date. In this paper a deterministic approximation algorithm with performance ratio of 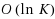$O(\ln K)$ for the min–max version of the problem is also proposed.