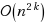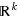A polynomial case of the cardinality‐constrained quadratic optimization problem

We propose in this paper a fixed parameter polynomial algorithm for the cardinality‐constrained quadratic optimization problem, which is NP‐hard in general. More specifically, we prove that, given a problem of size n (the number of decision variables) and s (the cardinality), if the n−k largest eigenvalues of the coefficient matrix of the problem are identical for some 0 < k ≤ n, we can construct a solution algorithm with computational complexity of $\mathcal{O}\left(n^{2k}\right)$ . Note that this computational complexity is independent of the cardinality s and is achieved by decomposing the primary problem into several convex subproblems, where the total number of the subproblems is determined by the cell enumeration algorithm for hyperplane arrangement in ${ℝ}^k$ space.