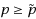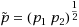On maximum order statistics from heterogeneous geometric variables

Let X 1,X 2 be independent geometric random variables with parameters p 1,p 2, respectively, and Y 1,Y 2 be i.i.d. geometric random variables with common parameter p. It is shown that X 2:2, the maximum order statistic from X 1,X 2, is larger than Y 2:2, the second order statistic from Y 1,Y 2, in terms of the hazard rate order [usual stochastic order] if and only if 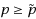$p\ge \stackrel{~<!--\; tilde\; -->}{p}$ , where 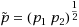$\stackrel{~<!--\; tilde\; -->}{p}=(p_1{p}_2{)}^{\frac{1}{2}}$ is the geometric mean of (p 1,p 2). This result answers an open problem proposed recently by Mao and Hu (2010) for the case when n=2.