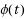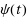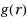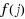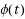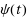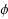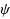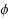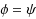Study of rank‐ and size‐frequency functions and their relations in a generalized Naranan framework

The Naranan formalism supposes that the number of sources and the number of items in sources grows exponentially. Here we extend this formalism by assuming, very generally, that the number of sources grows according to a function $\phi \left(t\right)$ and that the number of items in sources grows according to a function $\psi \left(t\right)$ . We then prove formulae for the rank‐frequency function $g\left(r\right)$ and the size‐frequency function $f\left(j\right)$ in terms of the function $\phi \left(t\right)$ and $\psi \left(t\right)$ . As a special case, we obtain Naranan’s original result that $f\left(j\right)$ is the law of Lotka if $\phi$ and $\psi$ are exponential functions. We also prove relations between the rank‐ and size‐frequency functions of two systems where the second system is built on the same functions $\phi$ and $\psi$ as the first system but in reverse order. Results of $\phi =\psi$ follow from this as a consequence.