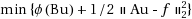Bregman operator splitting with variable stepsize for total variation image reconstruction

This paper develops a Bregman operator splitting algorithm with variable stepsize (BOSVS) for solving problems of the form 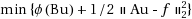$\min \{\varphi (\mathrm{Bu})+1/2\parallel \mathrm{Au}‐f{\parallel }_2^2\}$ , where ϕ may be nonsmooth. The original Bregman Operator Splitting (BOS) algorithm employed a fixed stepsize, while BOSVS uses a line search to achieve better efficiency. These schemes are applicable to total variation (TV)‐based image reconstruction. The stepsize rule starts with a Barzilai‐Borwein (BB) step, and increases the nominal step until a termination condition is satisfied. The stepsize rule is related to the scheme used in SpaRSA (Sparse Reconstruction by Separable Approximation). Global convergence of the proposed BOSVS algorithm to a solution of the optimization problem is established. BOSVS is compared with other operator splitting schemes using partially parallel magnetic resonance image reconstruction problems. The experimental results indicate that the proposed BOSVS algorithm is more efficient than the BOS algorithm and another split Bregman Barzilai‐Borwein algorithm known as SBB.