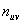This paper shows how to approximate, in the quickest and the most realistic possible way, the maximum of the sum of squares of a contingency table 
, with fixed margins. The trivial case, where the margins are not fixed, corresponds to the matrix structure known as ‘Complete Association’. For practical problems, no methods exist which guarantee an exact optimal solution. Bounds dues to mathematics inequality are proposed. This paper does not discuss the combinatory complexity of the problem but quotes with regard to Hubert and Arabie ‘à Constructing an exact bound, conditional on the fixed row and column totals of the given contingency table, is a very difficult problem of combinatorial optimizationà’ Lerman proposed a recursive algorithm, which determines step by step an optimal solution, based on the notion of ‘points extremaux’. Unfortunately the computing time increases exponentially. The paper proposes two bounds finer than those proposed in the literature. The distribution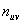 
corresponding to these bounds is not often reached. Then, the paper proposes a very fast heuristic procedure, based on classical assignment techniques, to find such optimal distribution.
