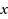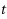Higher order perturbation expansion of waves in water of variable depth

In this work, we extended the application of ‘the modified reductive perturbation method’ to long waves in water of variable depth and obtained a set of KdV equations as the governing equations. Seeking a localized travelling wave solution to these evolution equations we determine the scale function $c_1\left(t\right)$ so as to remove the possible secularities that might occur. We showed that for waves in water of variable depth, the phase function is not linear anymore in the variables $x$ and $t$ . It is further shown that, due to the variable depth of the water, the speed of the propagation is also variable in the $x$ coordinate.