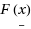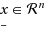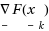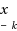On the convergence of trust region algorithms for unconstrained minimization without derivatives

We consider iterative trust region algorithms for the unconstrained minimization of an objective function 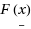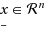$F(\underline{x})$ , $\underline{x}\in {ℛ}^n$ , when F is differentiable but no derivatives are available, and when each model of F is a linear or a quadratic polynomial. The models interpolate F at n+1 points, which defines them uniquely when they are linear polynomials. In the quadratic case, second derivatives of the models are derived from information from previous iterations, but there are so few data that typically only the magnitudes of second derivative estimates are correct. Nevertheless, numerical results show that much faster convergence is achieved when quadratic models are employed instead of linear ones. Just one new value of F is calculated on each iteration. Changes to the variables are either trust region steps or are designed to maintain suitable volumes and diameters of the convex hulls of the interpolation points. 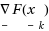It is proved that, if F is bounded below, if ∇² F is also bounded, and if the number of iterations is infinite, then the sequence of gradients $\underline{\nabla }F({\underline{x}}_k)$ , k=1,2,3,…, converges to zero, where 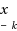${\underline{x}}_k$ is the centre of the trust region of the k‐th iteration.