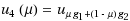Convergence of distributed optimal control problems governed by elliptic variational inequalities

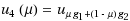First, let u g be the unique solution of an elliptic variational inequality with source term g. We establish, in the general case, the error estimate between $u_3(\mu )=\mu u_{g_1}+(1‐\mu )u_{g_2}$ and $u_4(\mu )=u_{\mu g_1+(1‐\mu )g_2}$ for μ∈[0,1]. Secondly, we consider a family of distributed optimal control problems governed by elliptic variational inequalities over the internal energy g for each positive heat transfer coefficient h given on a part of the boundary of the domain. For a given cost functional and using some monotony property between u 3(μ) and u 4(μ) given in Mignot (J. Funct. Anal. 22:130–185, 1976), we prove the strong convergence of the optimal controls and states associated to this family of distributed optimal control problems governed by elliptic variational inequalities to a limit Dirichlet distributed optimal control problem, governed also by an elliptic variational inequality, when the parameter h goes to infinity. We obtain this convergence without using the adjoint state problem (or the Mignot’s conical differentiability) which is a great advantage with respect to the proof given in Gariboldi and Tarzia (Appl. Math. Optim. 47:213–230, 2003), for optimal control problems governed by elliptic variational equalities.