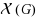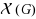| Article ID: | iaor20125995 |
| Volume: | 24 |
| Issue: | 4 |
| Start Page Number: | 459 |
| End Page Number: | 467 |
| Publication Date: | Nov 2012 |
| Journal: | Journal of Combinatorial Optimization |
| Authors: | Pardalos Panos, Behdani Behnam, Granata Donatella |
| Keywords: | graphs |
We address the complexity class of several problems related to finding a path in a properly colored directed graph. A properly colored graph is defined as a graph