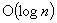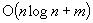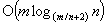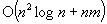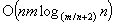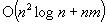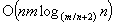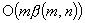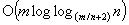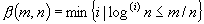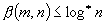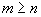In this paper the authors develop a new data structure for implementing heaps (priority queues). The present structure, Fibonacci heaps (abbreviated F-heaps), extends the binomial queues proposed by Vuillemin and studied further by Brown. F-heaps support arbitrary deletion from an n-item heap in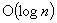 
amortized time and all other standard heap operations in O(1) amortized time. Using F-heaps the authors are able to obtain improved running times for several network optimization algorithms. In particular, they obtain the following worst-case bounds, where n is the number of vertices and m the number of edges in the problem graph: (1) 
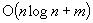for the single-source shortest path problem with nonnegative edge lengths, improved from 
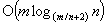; (2) 
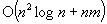for the all-pairs shortest path problem, improved from 
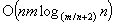; (3)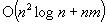 
for the assignment problem (weighted bipartite matching), improved from 
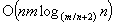; (4)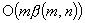 
for the minimum spanning tree problem, improved from 
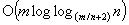, where 
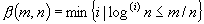. Note that 
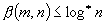if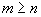 
. Of these results, the improved bound for minimum spanning trees is the most striking, although all the results give asymptotic improvements for graphs of appropriate densities.
