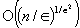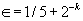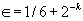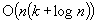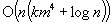The problem of scheduling a set of n jobs on m identical machines so as to minimize the makespan time is perhaps the most well-studied problem in the theory of approximation algorithms for NP-hard optimization problems. In this paper the strongest possible type of result for this problem, a polynomial approximation scheme, is presented. More precisely, for each ∈, an algorithm that runs in time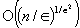 
and has relative error at most ∈ is given. In addition, more practical algorithms for 
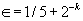and 
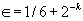, which have running times 
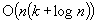and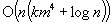 
are presented. The techniques of analysis used in proving these results are extremely simple, especially in comparison with the baroque weighting techniques used previously. The scheme is based on a new approach to constructing approximation algorithms, which is called dual approximation algorithms, where the aim is to find superoptimal, but infeasible, solutions, and the performance is measured by the degree of infeasibility allowed. This notion should find wide applicability in its own right and should be considered for any optimization problem where traditional approximation algorithms have been particularly elusive.
