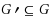On the probabilistic min spanning tree Problem

We study a probabilistic optimization model for min spanning tree, where any vertex v i of the input‐graph G(V, E) has some presence probability p i in the final instance G′⊂G that will effectively be optimized. Suppose that when this ‘real’ instance G′ becomes known, a spanning tree T, called anticipatory or a priori spanning tree, has already been computed in G and one can run a quick algorithm (quicker than one that recomputes from scratch), called modification strategy, that modifies the anticipatory tree T in order to fit G′. The goal is to compute an anticipatory spanning tree of G such that, its modification for any 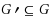$G\prime \subseteq G$ is optimal for G′. This is what we call probabilistic min spanning tree problem. In this paper we study complexity and approximation of probabilistic min spanning tree in complete graphs under two distinct modification strategies leading to different complexity results for the problem. For the first of the strategies developed, we also study two natural subproblems of probabilistic min spanning tree, namely, the probabilistic metric min spanning tree and the probabilistic min spanning tree 1,2 that deal with metric complete graphs and complete graphs with edge‐weights either 1, or 2, respectively.